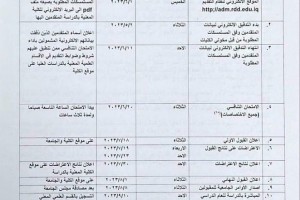
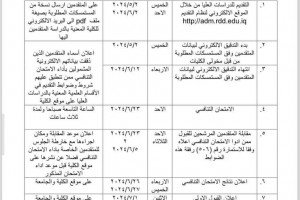
The College of Science, Department of Mathematics, discussed the master's thesis of student Mohammed Imad Abdul Karim, entitled "Two-Stage Hybrid Methods for Nonlinear Stochastic Differential Equations." The thesis reviewed two innovative hybrid methods for numerically solving nonlinear stochastic differential equations (SDEs): the fourth-order Chebyshev-Runge-Kutta method and the fourth-order Ito-corrected Chebyshev-Runge-Kutta method. The first method relies on approximating local Brownian increments using a Chebyshev polynomial, followed by the application of the classical fourth-order Runge-Kutta method. The second method employs the Ito-corrected formula for the drift term, followed by the application of a fourth-order Chebyshev-Runge-Kutta hybrid to incorporate higher-order random effects.