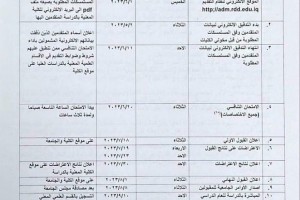
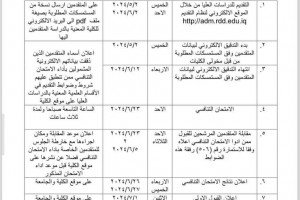
The College of Science in the Department of Mathematics discussed a seminar entitled Two-Stage Hybrid Methods for Nonlinear Stochastic Differential Equations for postgraduate student Mohammed E. Abd Al-Kareem. This seminar presents two innovative two-stage hybrid methods, the Chebyshev-RK4 method and the Itô-corrected Chebyshev-RK4 method, for the numerical resolution of nonlinear stochastic differential equations (SDEs). The first method, a Chebyshev-RK4 hybrid method, is formulated by approximating local Brownian increments at each macro-step with a fixed-degree Chebyshev polynomial, subsequently employing a classical fourth-order Runge-Kutta method on the outcome of the deterministic ordinary differential equation (ODE).  The second method employed the Itô -corrected form to augment the drift term with the Itô correction, followed by the application of the Chebyshev-RK4 hybrid to integrate higher-order stochastic effects.